CS:APP Cache Lab记录

前置知识

多级缓存

本质是基于代码运行时的时间局部性与空间局部性，往往顺序取指令，顺序访问内存中的元素，一段时间内选择的内存区域也往往相同。

具体流程

Part A

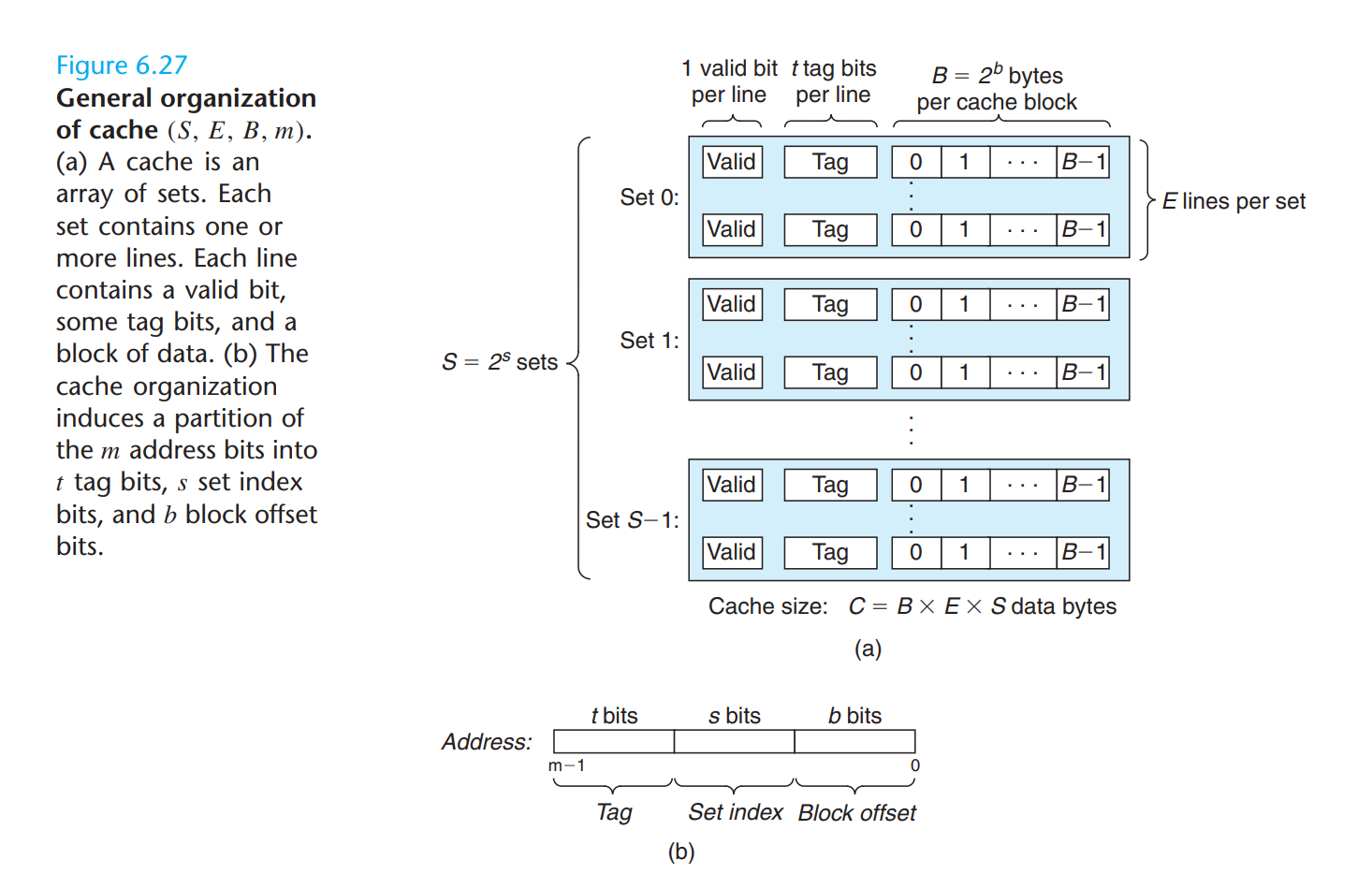
cache结构

在c语言的文件中模拟出以上结构的二级缓存。该实验只模拟数据Cache，因此忽视I开头的请求，只需要考虑L load，读取数据；S store 存储数据；M modify load 后 store。-v不必要但有助于debug

提取参数

需要有两个可选择的功能，四个必要的参数。若缺少参数时需要打印Usage、option，只要含有-h 只打印帮助。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// Get_opt API 处理不同参数的情况
// 注意if处理的先后对命令行的影响
// 比如在最后加入一个多余的参数，尽管其他条件都符合 都不会执行

//	if there exists -h
	// "Usage" 
	// return 0 

//	if there dosen't exist four valid mandatory parameters 
// 	? 缺少定义 重复定义 出现不合规的定义 -> 借助Get_opt处理  
	// "./csim: Missing required command line argument"
	// "Usage"
	// return 0  

//  if there exist invalid option
//	存在多余的参数
	// "./csim: invalid option -- 'f'" (order of apperance in command line)
	// "Usage" 
	// return 0	

//	if file not found
	// "traces/yi.trac: No such file or directory"
	// return 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
// c函数中处理输入的参数

// argc 参数的多少 至少非负

// 可以是**argv *argv[] 字符串数组
// ./main a b c
// argv[0] = ./main (相当于对命令行做拆分)

#include <unistd.h> 
int main(int argc, char *argv[]) {
	// getopt(int argc, char *const argv[], const char *optstring)
    // : required argument :: optional
    // 默认会进行排序，使得需要的参数在前面
    int arg, verbose = 0;
    int S, s = -1, E = -1, B, b = -1;
    char *path = NULL;
    FILE *fp;
    // C 打开文件并处理输入k
    // crefsim 没有做边界保护 "-1" 就会死循环
    // getopt 并不会强制判断哪些参数一定要存在    
    while ((arg = getopt(argc, argv, ":hvs:E:b:t:")) != -1) {
        switch (arg) {
            case 'h':
                outputUsage();                
                return 0;
                break;
            case 'v':
                verbose = 1;
                break;
            case 's':
                s = atoi(optarg);
                break;
            case 'E':
                E = atoi(optarg);
                break; 
            case 'b':
                b = atoi(optarg);
                break;
            case 't':
                // printf("%d\n", optind);
                path = argv[optind - 1];
                break;
            case ':':
                printf("%s: Missing required command line argument\n", argv[0]);
                outputUsage();
                return 0;
                break;
            default:
                printf("%s: invalid option -- '%c'\n", argv[0], optopt);
                outputUsage();
                return 0;
                break;
        }
    }
    if (s <= 0 || E <= 0 || b <= 0 || path == NULL) {
        printf("%s: Missing required command line argument\n", argv[0]);
        outputUsage();
        return 0;
    }
    fp = fopen(path, "r");
    if (!fp) {
        printf("%s: No such file or directory\n", path); 
        return 0;
    }
    solve(s, E, b, fp, verbose);
    return 0;
}

LRU实现

记录每组的最后遍历时间，O(n^2)，冗余的堆可以降低时间复杂度到 O(nlogn)， 到达的一定在最右侧，替换的在最左侧，冗余的队列也可以将时间复杂度降低到O(n)，到空间复杂度也是O(n)。

也可以利用哈希表直接定位，然后借助双端队列达到O(n)，可以保证空间严格在O(capacity)。

这里C直接使用基本的数据结构（没有哈希表）

注意用unsigned int， 参数过多...

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int checkHit(unsigned int **data, unsigned int **rec, unsigned int  cnt, unsigned int  E, unsigned int  sid, unsigned int  caddr) {
    for (unsigned int  i = 0; i < E; i++) {
        if (data[sid][i] == caddr) {
            rec[sid][i] = cnt;
            return 1;
        }
    }
    return 0;
}

unsigned int  checkEvict(unsigned int **rec, unsigned int **data, unsigned int  E, unsigned int  cnt, unsigned int  sid, unsigned int  caddr) {
     unsigned int  csign = 0;
     for (unsigned int  i = 0; i < E; i++) {
         if (rec[sid][i] == 0) {
             csign = 1;
             rec[sid][i] = cnt;
             data[sid][i] = caddr;
             break;
         }
     } 
     if (!csign) {
         unsigned int  cv = rec[sid][0], cid = 0;
         for (unsigned int  i = 1; i < E; i++) {
             if (rec[sid][i] < cv) {
                 cv = rec[sid][i];
                 cid = i;
             }
         }
         data[sid][cid] = caddr;
         rec[sid][cid] = cnt;
         return 1;
     }
     return 0;
}

主体的solve函数，注意代码命名的规范。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
void solve(unsigned int  s, unsigned int  E, unsigned int  b, FILE *fp, unsigned int  verbose) {
    unsigned int  S = 1 << s;
    char type;
    unsigned int  addr, sz; 
    unsigned int  hits = 0, misses = 0, evictions = 0;
    unsigned int  cnt = 1;

    unsigned int  **rec = (unsigned int **)malloc(sizeof(unsigned int *)*S);
    unsigned int  **data = (unsigned int **)malloc(sizeof(unsigned int *)*S);

    for (unsigned int  i = 0; i < S; i++) {
        rec[i] = (unsigned int *)malloc(sizeof(unsigned int )*E);
        data[i] = (unsigned int *)malloc(sizeof(unsigned int )*E);
        for (unsigned int  j = 0; j < E; j++) {
            rec[i][j] = 0;
            data[i][j] = -1;
        }
    } 

    while (fscanf(fp, " %c %x,%d", &type, &addr, &sz) != EOF) {
        if (verbose == 1) print f("%c %x,%d \n", type, addr, sz);
        if (type == 'I') continue;
        unsigned int  sid = (addr >> b) % S, caddr = addr >> b;
        // if (verbose == 1) prunsigned int f("%c %x,%d %d %d ", type, addr, sz, sid, caddr);
        if (type == 'L' || type == 'S') {
            if (checkHit(data, rec, cnt, E, sid, caddr)) {
                hits++;
                if (verbose == 1) print f("hit ");
            }
            else {
                misses++;
                if (verbose == 1) print f("miss ");
                unsigned int  prev = evictions;
                evictions += checkEvict(rec, data, E, cnt, sid, caddr);
                if (prev < evictions) {
                    if (verbose == 1) pint f("eviction");
                }
            }
        }
        if (type == 'M') { 
            hits++;
            if (checkHit(data, rec, cnt, E, sid, caddr)) {
                hits++;
                print f("hit hit");
            }
            else {
                misses++;
                printf("miss ");
                unsigned int  prev = evictions;
                evictions += checkEvict(rec, data, E, cnt, sid, caddr);
                if (evictions > prev) {
                    if (verbose == 1) printf("eviction ");
                }
                printf("hit");
            }
        }
        printf("\n");
        cnt++;
    }
    
    printSummary(hits, misses, evictions);

    for (unsigned int i = 0; i < E; i++) {
        free(rec[i]);
        free(data[i]);
    }
    free(rec);
    free(data);
}

注意make函数-std=c99会报错，且printSummary 不需要重复定义。

Part B

32个组，里面包含8个INT。

try1

首先尝试分块，不能假定数组每一块所处的Cache，但相邻块位于不同的Cache。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
    int G = 8;
    if (M == 64) G = 4;
    int tr = (M + G - 1) / G, tc = (N + G - 1) / G;
    for (int i = 0; i < tr; i++) {
        for (int j = 0; j < tc; j++) {
            int sl = i * G, el = min(M - 1, (i + 1) * G - 1);
            int sr = j * G, er = min(N - 1, (j + 1) * G - 1);
            for (int k = sr; k <= er; k++) {
                for (int l = sl; l <= el; l++) {
                    B[l][k] = A[k][l];
                }
            }
        }
    }          
}

结果

1
2
3
4
5
6
7
Cache Lab summary:
                        Points   Max pts      Misses
Csim correctness          27.0        27
Trans perf 32x32           6.9         8         343
Trans perf 64x64           1.8         8        1843
Trans perf 61x67          10.0        10        1913
          Total points    45.7        53

可以分开考虑，分开优化。可以看到具体的hit / miss。

？理论 8 * 8 块中一定会有6次Hit，考虑B的第一行 MISS MISS HIT ... ，B的第二行 MISS MISS MISS HIT ...， B的第三行 MISS HIT MISS MISS HIT HIT ... 至多三个MISS，第一次没有遍历过，第二次被A占用，写入后可能仍被A占用，第三次重新占用A。因此对于B最坏的情况 8 * 8 中 MISS 3 * 8，而对于A而言 MISS ... 被B占用 MISS ... !!! 前提是A B的每一列属于不同的CACHE，若满足以上情况，则MISS数为 16 * 5 * 8 = 640 343 倒也合理，若64 * 64也满足则会降低到 640 * 4 = 2560 (MAX)

1
2
3
4
5
6
7
8
9
64 * 64 
8个INT，4 * 8 = 32 第五行与第一行位于同一个Cache
所以这里不能使用 8 * 8 的块，可以使用 4 * 4 的块
   5 L 10d080,4 miss eviction
   6 S 14d080,4 miss eviction
   
从同一个Cache开始
10d080
14d080

try2

！平均每一块允许MISS的次数 1.17 32 * 32，1.27 64 * 64，因此被占用的次数只能是常数级别，8 * 8 的块可以 Miss 2次

  • 思路一：改变分块的形状或不分块？ 若要复用读入A中的元素，一定会导致读入B中的多块，而若要复用B中的多块，又需要读入A中的多块。

  • 思路二：在 8 * 8 或 4 * 4 的内部块进行赋值的优化

    把处于相同Cache的赋值放到最后，借助临时的变量传递。计算出当前列与当前Cache占用相同块的行号。映射出Cache号。参数较多都可以优化到小于12个，这里便于表示。

  • 思路三：牺牲时间复杂度

    一定需要读入8 * 8 的分块，意义不大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N]) {
    int dx = 8, dy = 8;
    if (M == 64) dx = 4, dy = 4;
    int tr = (M + dx - 1) / dx, tc = (N + dy - 1) / dy;
    if (M == 32 || M == 64) {
        for (int i = 0; i < tr; i++) {
            for (int j = 0; j < tc; j++) {
                int sl = i * dx, el = min(M - 1, (i + 1) * dx - 1);
                int sr = j * dy, er = min(N - 1, (j + 1) * dy - 1);
                for (int k = sr; k <= er; k++) {
                    int cc = ((k * M + sl) / 8) % 32;
                    int gsign = 0, gv = 0, gy;
                    for (int l = sl; l <= el; l++) {
                        int nc = ((l * N + k) / 8) % 32;
                        // 若Cache相同则先不赋值
                        // 确保A当前行的遍历没问题
                        // A一定会占据一个B的Cache，可以等该Cache读入后顺便赋值。
                        if (nc == cc) {
                            gsign = 1;
                            gv = A[k][l];
                            gy = l;
                            continue;
                        }
                        B[l][k] = A[k][l];
                    }
                    if (gsign) B[gy][k] = gv;
                }

            }
        }
        return;
    }         
}

结果

1
2
3
4
5
6
7
Cache Lab summary:
                        Points   Max pts      Misses
Csim correctness          27.0        27
Trans perf 32x32           8.0         8         287
Trans perf 64x64           4.0         8        1651
Trans perf 61x67          10.0        10        1913
          Total points    49.0        53

ans

没想到可以直接复制一行/一列 8个作为参数，计算Cache号数的方式也比较取巧。滥用参数的下场... 循环只占了3 - 4 个参数，只取决与嵌套的深度。核心的逻辑在于：

  • 一次性 横向读入 A1 A2 A3 A4 纵向写入 B1 B2 B3 B4 （同时使得转移的过程中可以横向读入，这里B1 B2 B3 B4 可能因为与A1 A2 A3 A4的Cache冲突多Miss一次）
  • 横向读入B1 暂存部分 (B1此时一定在Cache中)，一次性纵向读入 A5 A6 A7 A8，读回到B1，同时读入B5，一定覆盖B1。（这里B1可能因为读入A5 A6 A7 A8 多MISS一次，A5 同理）
  • 横向读入 A5 A6 A7 A8， 纵向写入 B5 B6 B7 B8。
  • 能够最优的前提在于 A B不占用同一个Cache的情况。

解答链接

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
void transpose_64x64(int M, int N, int A[N][M], int B[M][N])
{
    int a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7;
    for (int i = 0; i < 64; i += 8){
        for (int j = 0; j < 64; j += 8){
            for (int k = i; k < i + 4; k++){
                // 得到A的第1,2块
                // 用了Cache A1号
                a_0 = A[k][j + 0];
                a_1 = A[k][j + 1];
                a_2 = A[k][j + 2];
                a_3 = A[k][j + 3];
                a_4 = A[k][j + 4];
                a_5 = A[k][j + 5];
                a_6 = A[k][j + 6];
                a_7 = A[k][j + 7];
                // 复制给B的第1,2块
                // 用了Cache B1 B2 B3 B4
                // 正确的
                B[j + 0][k] = a_0;
                B[j + 1][k] = a_1;
                B[j + 2][k] = a_2;
                B[j + 3][k] = a_3;
                
                // 暂存
				B[j + 0][k + 4] = a_4;
                B[j + 1][k + 4] = a_5;
                B[j + 2][k + 4] = a_6;
                B[j + 3][k + 4] = a_7;
            }
            // Cache B1 B2 B3 B4 传输完成
            
            for (int k = j; k < j + 4; k++){
                // 得到B的第2块
            	// 使用 B1
                a_0 = B[k][i + 4];
                a_1 = B[k][i + 5];
                a_2 = B[k][i + 6];
                a_3 = B[k][i + 7];
                
                // 读入A5
                a_4 = A[i + 4][k];
                a_5 = A[i + 5][k];
                a_6 = A[i + 6][k];
                a_7 = A[i + 7][k];
                
                // 复制给B的第2块
                B[k][i + 4] = a_4;
                B[k][i + 5] = a_5;
                B[k][i + 6] = a_6;
                B[k][i + 7] = a_7;
                
                // B原来的第2块移动到第3块
                // 同时覆盖B1
                B[k + 4][i + 0] = a_0;
                B[k + 4][i + 1] = a_1;
                B[k + 4][i + 2] = a_2;
                B[k + 4][i + 3] = a_3;
            }
            for (int k = i + 4; k < i + 8; k++)
            {
                // 处理第4块
                a_4 = A[k][j + 4];
                a_5 = A[k][j + 5];
                a_6 = A[k][j + 6];
                a_7 = A[k][j + 7];
                B[j + 4][k] = a_4;
                B[j + 5][k] = a_5;
                B[j + 6][k] = a_6;
                B[j + 7][k] = a_7;
            }
        }
    }
}

小结

  1. 代码习惯

    • Part A没有建立数据结构，导致函数传参的复杂。

    • Part B 设置了一些没必要的参数，以至于没意识到12个参数的意义在于可以复制一整列 / 行。

  2. Cache替换

    • 两个数组起始所占的Cache行号是否相同
    • 二位数组不同行之间的Cache行号是否相同
    • 每读入一个Cache块，能够做到的最少被占用的次数。
    • 具体到二维数组的转置，在知道Cache块大小和Cache行数的情况下，可以做针对性的优化。
    • 因此一般而言，设置大小适中的block有一定概率能够提高程序运行的速度。
    • 以块的整个周期来分析平均MISS的次数，以此推断整体的MISS。
CS

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！