机器学习基础

实验概述

1. 基于帖子^[1]的代码与框架，通过python numpy库构建基本的神经网络模型，在基本结构的基础上增加了mini-batch梯度下降，针对多标签问题，使用softmax作为输出层的激活函数，cross entropy定义损失函数。
2. 使用MNIST数据集检验建立的模型，设立合适的神经网络层数，batch个数，学习率，epoch等参数，限于算力，只尝试了较为小的模型，并通过训练测试准确率曲线观察训练效果。
3. 基于官方文档^[2]的代码与框架，通过pytorch建立CNN模型，与简单神经网络做比对，观察效果。

基本神经网络

基本结构

# 基本结构
NN_ARCHITECTURE = [
    # 输入->隐藏层1的权重
    {"input_dim": 784, "output_dim": 500, "activation": "relu"},
    # 隐藏层1->隐藏层2的权重
    {"input_dim": 500, "output_dim": 150, "activation": "relu"},
    # 隐藏层2->输出的权重
    {"input_dim": 150, "output_dim": 10, "activation": "softmax"},
    # {"input_dim": 50, "output_dim": 10, "activation": "softmax"}
]

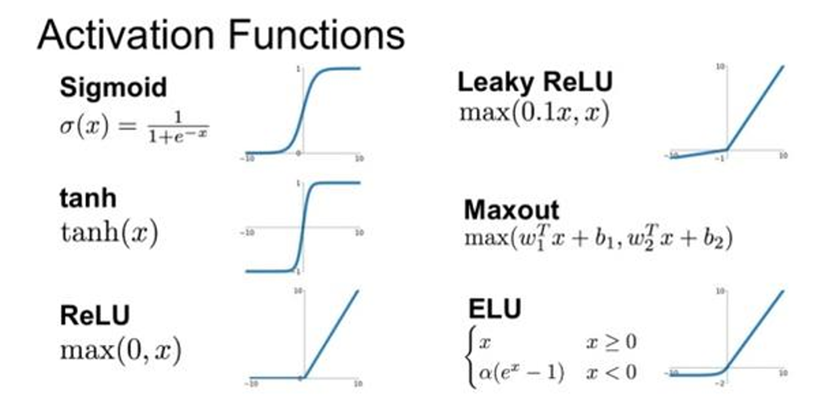
激活函数

激活函数为神经网络增添了非线性，能够拟合更复杂的模型。且选择合适的激活函数可以防止梯度爆炸与梯度消失，本文使用relu作为默认的激活函数。

def sigmoid(Z):
    return 1/(1+np.exp(-Z))

def relu(Z):
    return np.maximum(0,Z)

def sigmoid_backward(dA, Z):
    sig = sigmoid(Z)
    return dA * sig * (1 - sig)

def relu_backward(dA, Z):
    dZ = np.array(dA, copy = True)
    dZ[Z <= 0] = 0
    return dZ

def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=0, keepdims=True))
    return exp_x / np.sum(exp_x, axis=0, keepdims=True)

def softmax_backward(y_hat, y):
    m = y.shape[0]
    dx = y_hat.T.copy()
    dx[range(m), y.T] -= 1
    dx /= m
    return dx.T

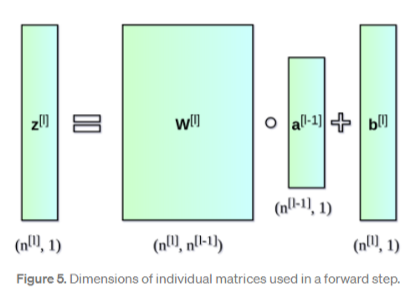
前向传播

设每一层的输出为\(a^l\), 则有\(z^{l} = W^l \cdot a^{l - 1} + b^{l}, a^{l} = g^{l}(z^{l})\), 如下图所示。

# 代码实现

def single_layer_forward_propagation(A_prev, W_curr, b_curr, activation="relu"):
    
    # np.dot即为矩阵乘法
    Z_curr = np.dot(W_curr, A_prev) + b_curr
    
    # selection of activation function
    if activation == "relu":
        activation_func = relu
    elif activation == "sigmoid":
        activation_func = sigmoid
    elif activation == "softmax":
        activation_func = softmax
    else:
        raise Exception('Non-supported activation function')
        
    return activation_func(Z_curr), Z_curr

def full_forward_propagation(X, params_values, nn_architecture):
    # 保留缓存
    memory = {}
    # X vector is the activation for layer 0 
    A_curr = X
    
    for idx, layer in enumerate(nn_architecture):

        layer_idx = idx + 1
        
        # 上一层的输入
        A_prev = A_curr
        
        # 当前使用的激活函数r
        activ_function_curr = layer["activation"]
        
        # 当前的W, b
        W_curr = params_values["W" + str(layer_idx)]
        b_curr = params_values["b" + str(layer_idx)]
        
        # 计算当前的A, Z
        A_curr, Z_curr = single_layer_forward_propagation(A_prev, W_curr, b_curr, activ_function_curr)
        
        # 保存用作后向传播
        memory["A" + str(idx)] = A_prev
        memory["Z" + str(layer_idx)] = Z_curr
       
    return A_curr, memory

损失函数

定义损失函数，损失函数越小，代表预测值越精准，对于回归问题，可以使用RMSE作为损失函数，而对于分类问题，采用sigmoid + binary_cross_entropy的方式或log_softmax方式，考虑到softmax方法考虑到了每个元素之间的关系，在多标签问题有一定的优势，本文采用soft_max结合Cross_Entropy_Loss的方式。

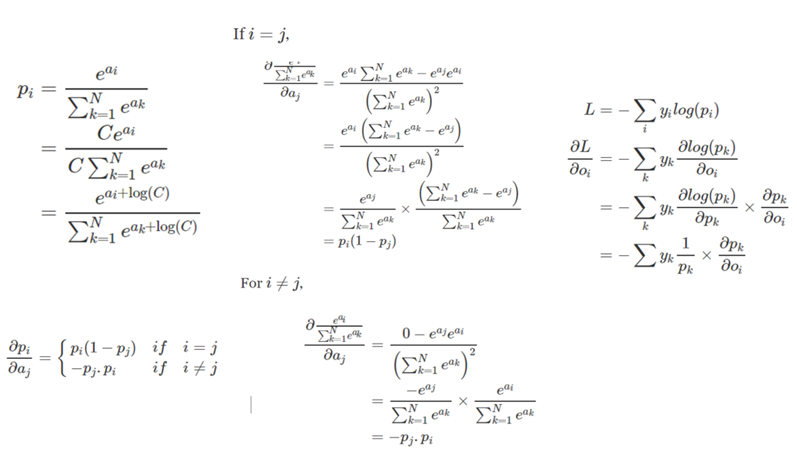
公式证明:

def softmax_backward(y_hat, y):
    m = y.shape[0]
    dx = y_hat.T.copy()
    dx[range(m), y.T] -= 1
    dx /= m
    return dx.T

def cross_entropy_loss(y_hat,y):
    m = y.shape[0]
    log_likelihood = -np.log(y_hat.T[range(m),y.T])
    loss = np.sum(log_likelihood) / m
    return loss

pytorch则直接使用log_softmax + NLLLoss作为损失函数。

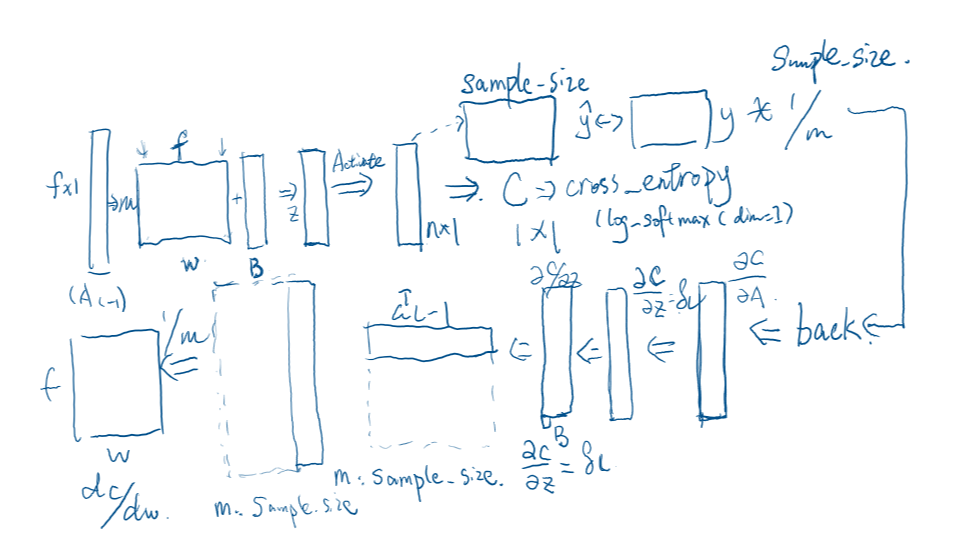
后向传播

通过梯度下降结合学习率更新值。 \[ x' = x - \alpha \frac{dy}{dx} \]

示意图：

公式证明:

def single_layer_backward_propagation(dA_curr, W_curr, b_curr, Z_curr, A_prev, activation="relu"):

    m = A_prev.shape[1]
    
    # dC/dA -> DC/dZ
    if activation == "relu":
        backward_activation_func = relu_backward
    elif activation == "sigmoid":
        backward_activation_func = sigmoid_backward
    elif activation == "softmax":
        backward_activation_func = softmax_backward
    else:
        raise Exception('Non-supported activation function')
    
    if (activation == "softmax"):
        dZ_curr = dA_curr
    else:
        dZ_curr = backward_activation_func(dA_curr, Z_curr)
        
    # 计算dw
    dW_curr = np.dot(dZ_curr, A_prev.T) / m
    # 作为下一轮的dC/dA
    db_curr = np.sum(dZ_curr, axis=1, keepdims=True) / m
    # derivative of the matrix A_prev
    dA_prev = np.dot(W_curr.T, dZ_curr)

    return dA_prev, dW_curr, db_curr


def full_backward_propagation(Y_hat, Y, memory, params_values, nn_architecture):
    grads_values = {}

    m = Y.shape[0]

    dA_prev = softmax_backward(Y_hat, Y)
    
    for layer_idx_prev, layer in reversed(list(enumerate(nn_architecture))):
        layer_idx_curr = layer_idx_prev + 1

        activ_function_curr = layer["activation"]
        
        dA_curr = dA_prev
        
        # 上一轮的A
        A_prev = memory["A" + str(layer_idx_prev)]
        Z_curr = memory["Z" + str(layer_idx_curr)]
        
        W_curr = params_values["W" + str(layer_idx_curr)]
        b_curr = params_values["b" + str(layer_idx_curr)]
        
        dA_prev, dW_curr, db_curr = single_layer_backward_propagation(
            dA_curr, W_curr, b_curr, Z_curr, A_prev, activ_function_curr)
        
        # 保留对应的梯度值
        grads_values["dW" + str(layer_idx_curr)] = dW_curr
        grads_values["db" + str(layer_idx_curr)] = db_curr
    
    return grads_values

训练方式

使用mini-batch训练，batch size选择128，较SGD时间复杂度较小，较batch训练增加了random shuffle，且多组训练，有助于寻找全局最优。

for i in range(epochs):
    p = np.random.permutation(train_label.shape[0])
    train_data= train_data.T[p].T
    train_label = train_label[p]
    start = 0
    batch = 128
    while (start < train_data.shape[1]):
        #...
        start += batch	

训练Mnist数据集

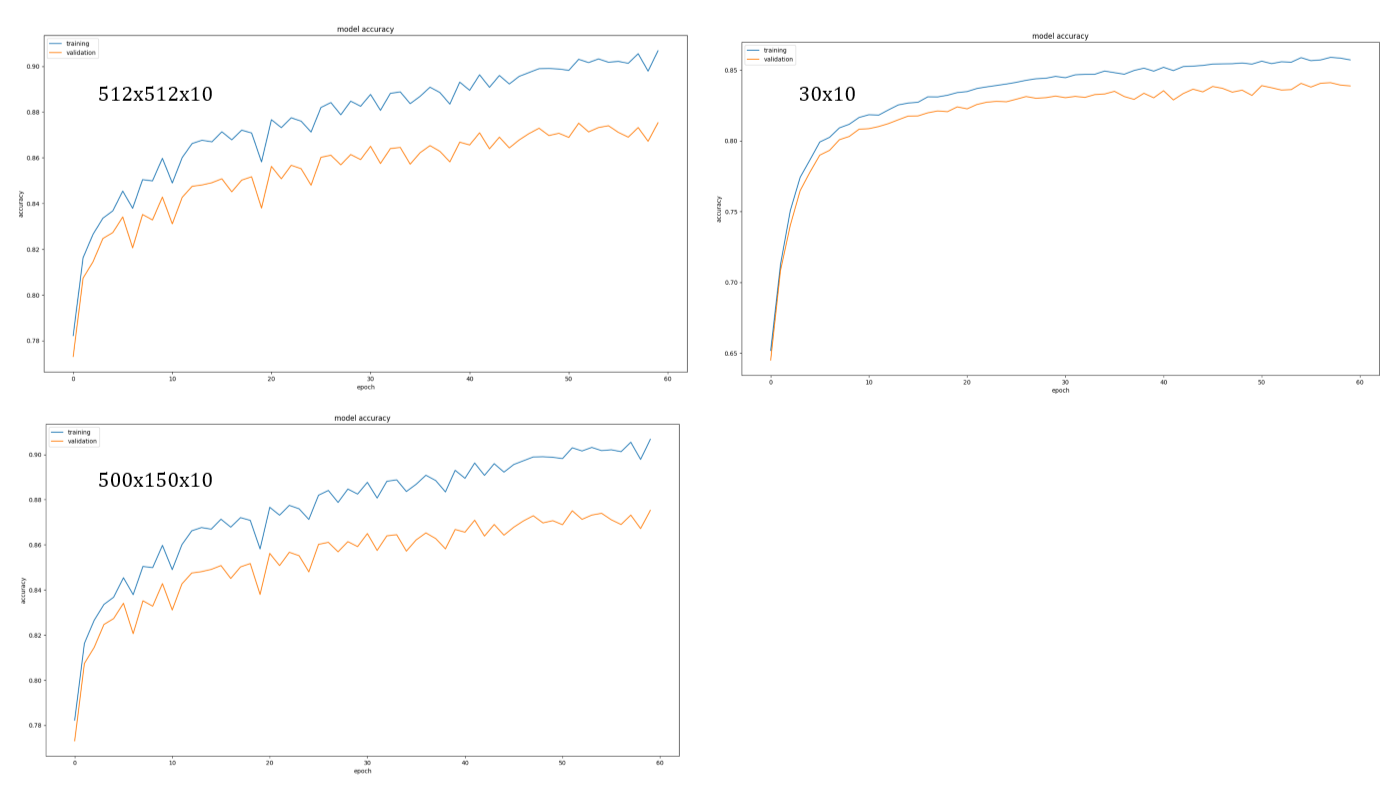
训练测试曲线

size	train accuracy	test accuracy
512x512x10	0.94	0.88
500x150x10	0.90	0.87
30x10	0.86	0.83

可以看出使用512x512x10的网络训练集与测试集的准确率相差较大，体现出过拟合的特点，500x150x10表现也较为相近。而30x10的网络训练和测试误差都较大，可以体现出欠拟合的特点。但整体网络的效果较差，由于针对图像数据，将图像的每个像素作为features, 并不能很好的体现图像的特点，而是用卷积神经网络可以解决这个问题。

使用CNN模型

参考^[2]，通过pytorch快速建立CNN模型，并设置droupout正则化防止过拟合。CNN模型通过卷积核更直观的展现图像各个区域的特点，且起到了降维的作用，而后面的全连接层则可将前面通过卷积抽象出的特征进行分类训练，较上文直接使用像素作为特征更有意义，准确率也更高。

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, 3, 1)
        self.conv2 = nn.Conv2d(32, 64, 3, 1)
        self.dropout1 = nn.Dropout(0.25)
        self.dropout2 = nn.Dropout(0.5)
        self.fc1 = nn.Linear(9216, 128)
        self.fc2 = nn.Linear(128, 10)

    def forward(self, x):
        x = self.conv1(x)
        x = F.relu(x)
        x = self.conv2(x)
        x = F.relu(x)
        x = F.max_pool2d(x, 2)
        x = self.dropout1(x)
        x = torch.flatten(x, 1)
        x = self.fc1(x)
        x = F.relu(x)
        x = self.dropout2(x)
        x = self.fc2(x)
        output = F.log_softmax(x, dim=1)
        return output

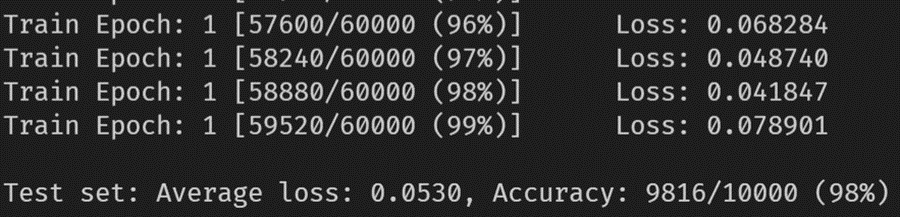
CNN训练结果

可以看出，只经过一个epoch就在测试集达到了98准确率，体现了CNN网络解决图像识别问题的能力。

1. https://towardsdatascience.com/lets-code-a-neural-network-in-plain-numpy-ae7e74410795 ↩︎
2. https://github.com/pytorch/examples/blob/main/mnist/main.py ↩︎