A survey on 5G channel encoding technology

Abstract

This article begins by explaining the meaning, motivation, and development of channel encoding. The concepts of two modern 5G code systems, particularly polar codes, are then discussed, along with their pros and downsides. Following that, the international standard and application scenarios for current codes are presented. China's participation is also highlighted. Finally, it depicts the channel coding technology's future trends.

Introduction

Basis

One of the source encoder's functions, as mentioned in Source encoding, is to remove unnecessary binary digits from the digitized signal. The channel encoder's technique, on the other hand, is to provide redundancy to the broadcast signal in order to repair errors caused by noise during transmission at the receiver. Error-control coding is a method of encoding that protects against channel errors. Satellite communication, deep-space communication, mobile radio communication, and computer networking are all applications that require error-control codes.

There are two generally used ways of preventing errors in electronically transferred data. Forward error control is one way (FEC). Information bits are secured against errors in this approach by transmitting extra redundant bits, which can be used by the decoder to detect where errors occurred and how to rectify them if they occur during transmission. The automatic repeat request method is the second approach to error control (ARQ). This method involves adding redundant bits to the transmitted data, which the recipient uses to detect errors. A request for a repeat broadcast is then sent by the recipient.

To control errors, we can employ repetition codes, the Hamming code, and convolutional encoding. Repetition codes simply work by sending each data bit three times. Because the information is blocked into finite-length bit sequences to which a number of superfluous bits are added, the Hamming code is called a block code. When a block encoder receives k information bits, n k redundancy bits are appended to the information bits to create a transmitted code word of n bits. One block of k information bits can so determine the entire code word of length n. As to convolutional encoding, the encoder output is an endless stream of bits rather than being naturally split into chunks. Memory is used in convolutional encoding such that the encoder output is determined by the previous M blocks of k information bits combined with the current block of k information bits.

Motivation

The digital signal will create error codes during transmission due to the noise in the mobile communication system. To improve system reliability, a variety of methods (use error correction/error detection coding technology, increase the signal transmission power, etc.) are required to improve signal and reduce the system error rate.

There are numerous benefits to using a higher-performing channel encoding method.

1. Noise and interference rise when more data is delivered across a network. Better error correction helps the system to withstand the higher errors caused, allowing for more capacity and, as a result, lower per-user costs.
2. Channel coders and decoders with higher performance can handle higher data rates, resulting in increased throughput.
3. Increasing the wireless link's efficiency lowers the power needs at both the base station and the user's device, resulting in longer battery life.

Development History

The field of channel coding started with Claude Shannon’s 1948 landmark paper. Its main goal for the next half-century was to develop viable coding systems that approached the Shannon limit on a few well-understood channels, such as the additive white Gaussian noise channel.

There was always a 2 to 3dB gap between the designed system gain and Shannon theoretical limit before the Turbo code was discovered. Turbo code is also known as parallel concatenated convolutional code. Turbo Codes and Tail Bitting Convolution Codes (TBCC) have proven to be efficient for LTE communication. Turbo code has been widely used in mobile communication technology. This technique is used for channel coding from 3G to 4G and even 4.5G. Two convolutional encoders, two serial decoders, and one interleaver are used in Turbo codes. Turbo codes receive their name from a revolutionary feedback loop they use that, at least conceptually, works in the same way that turbo exhaust systems do in cars. The actual novelty in turbo codes is in the cleverness with which soft data is used. Prior systems required hard knowledge of the received bits (e.g., 0s or 1s). Turbo codes, on the other hand, simply require a probabilistic assessment of each bit to be correctly decoded. This effectively permits much more data to be transmitted through turbo code channels.

However, Turbo code has many iterations and a large decoding delay, which is difficult to meet the network requirements of 5G with high speed and low delay. These codes failed to meet the requirements for 5G communications. To meet the requirements of 5G communications, LDPC and Polar codes are used for error correction.

When Gallager first created LDPC codes in 1963, they were impractical to apply and were forgotten until his work was rediscovered in 1996. Turbo codes, another class of capacity-approaching codes developed in 1993, became the de facto coding scheme in the late 1990s, with applications such as the Deep Space Network and satellite communications. Low-density parity-check codes, on the other hand, have surpassed turbo codes in terms of error floor and performance in the higher code rate range, leaving turbo codes suitable exclusively to lower code rates.

Polar codes were invented in 2009 by Erdal Arikan. They are the first family of error-correcting codes that achieve the Shannon capacity. In October 2016, Huawei announced that in 5G field trials using polar codes for channel coding, it achieved 27 G bit/s. The improvements have almost bridged the gap between channel performance and the Shannon limit, which defines the highest rate for a given bandwidth and noise level.

Key Technology

Channel capacity

Channel capacity indicates the theoretical maximum amount of information that can be transmitted in a channel. \[ \begin{align*} & R = I(X;Y) = H(X)- H(X|Y) \\ & C = \max_{p(a_i)}I(X;Y) \\ \end{align*} \] Shannon theorem indicates that the capacity of the channel with noise is related to the bandwidth and signal-to-noise ratio of the transmission channel under certain bandwidth. \[ C = 2B\log_2({1 + \frac{S}{N}}) \] Shannon also pointed out that if the information rate R is not greater than the communication channel's capacity C, a coding approach might be used to achieve the reliable transmission of information. However, the Shannon theorem does not specify how this system can be implemented.

LDPC codes

LDPC (Low-density parity-check code) was first proposed by Gallager in 1962. The initial theory of LDPC is based on binary domain, that is, binary LDPC. With further research on LDPC, LDPC is extended to a multivariate domain, namely multivariate LDPC. Binary LDPC has been widely used in the field of communication and broadcasting, and the research on multivariate LDPC has achieved remarkable results.

A sparse Tanner graph subclass of the bipartite graph is used to create an LDPC. A Tanner graph is a bipartite graph named after Michael Tanner that is used to express constraints or equations that specify error-correcting codes. Theoretical coding Tanner graphs are used to combine smaller codes into longer ones. These graphs are used extensively by both encoders and decoders.

LDPC codes are capacity-approaching codes, which means that practical constructions exist that allow the noise threshold to be set very close to the theoretical maximum (the Shannon limit) for a symmetric memoryless channel. The noise threshold defines an upper bound for the channel noise, up to which the probability of lost information can be made as small as desired.

Belief propagation, also known as sum-product message passing, is a message-passing method used to infer from graphical models like Bayesian networks and Markov random fields. It determines the marginal distribution for each unseen node (or variable) based on any observed nodes (or variables). Belief propagation is widely employed in artificial intelligence and information theory, with empirical success in a variety of applications such as low-density parity-check codes, turbo codes, free energy approximation, and satisfiability.

Using iterative belief propagation techniques, LDPC codes can be decoded in time linear to their block length.

Polar codes

Polar codes depend on channel polarization and are the first provable code construction to achieve Shannon capacity for arbitrary symmetric binary input channels. It has lower complexity and improved BER (Bit Error Ratio) performance. And it includes high-performance error correction technology. And most importantly, polar codes do not exhibit the error flow behavior, which means a higher SNR will definitely result in a lower error rate.

Using a simple example from the lecture^[1], we can quickly gain an intuitive understanding of the polar code.

BEC (Binary Erasure Channel) is a channel in which a transmitter sends a bit (a zero or a one), and the receiver either gets the bit correctly or receives a message indicating that the bit was not received ("erased") with a certain probability $ $. As shown in the picture.

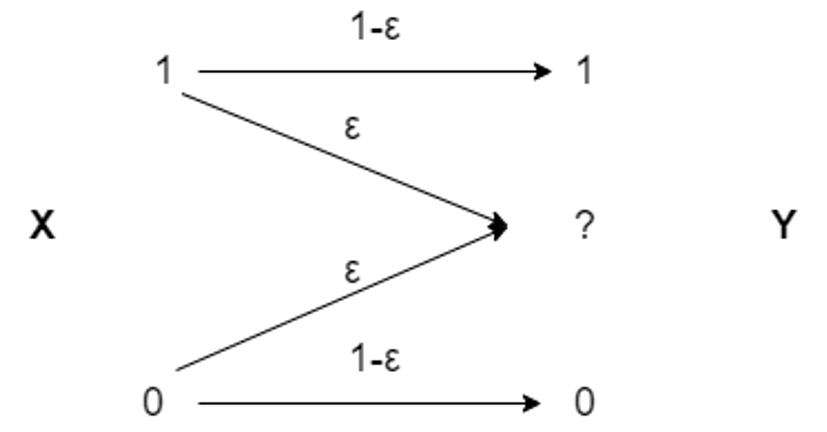
The simplest case of polar code is considered first. The process of Chanel Polarization is shown in the diagram below when the code length is two.

polarization

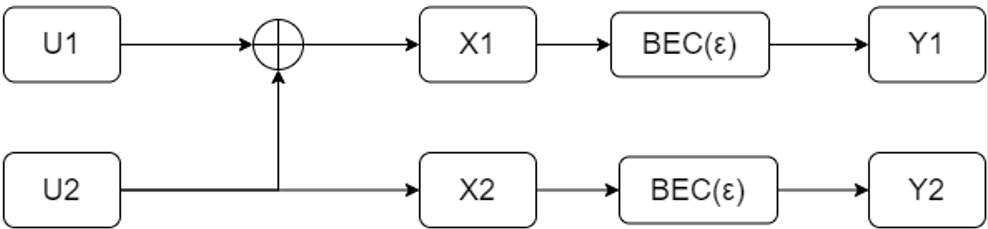
The decoding of U1 is as follows \[ \begin{equation} U_1 = \begin{cases} Y_1 \oplus Y_2, & \text{if } Y_1, Y_2 \in \left\{ 0, 1 \right\}\\ \text{?} \oplus Y_2, & \text{if } Y_1 =\text{?}, Y_2 \in \left\{ 0, 1 \right\}\\ Y_1 \oplus \text{?}, & \text{if } Y_1 \in \left\{ 0, 1 \right\}, Y_2=\text{?}\\ \text{?} \oplus \text{?}, & \text{if } Y_1=\text{?}, Y_2 =\text{?}\\ \end{cases} \end{equation} \] As shown in the equation, the receiver can get the U1 information only when both Y1 and Y2 are sent successfully. If we consider the transition of U1 as channel 1, the erasure probability is \[ P_1 = 1 - (1-\epsilon)^2 = 2\epsilon-\epsilon^2 \] Assuming that U1 transmission is successful, the sending of U2 is \[ \begin{equation} U_2 = \begin{cases} Y_1 \oplus U_1, & \text{if } Y_1\in \left\{ 0, 1 \right\}\\ Y_2, & \text{if } Y_2 \in \left\{ 0, 1 \right\}\\ \text{?}, & \text{if } Y_1 = Y_2=\text{?}\\ \end{cases} \end{equation} \] As shown in the equation, the receiver can't get the U1 information only when both Y1 and Y2 are sent unsuccessfully. If we consider the transition of U2 as channel 2, the erasure probability is \[ P_2 = \epsilon^2 \\ \] After the above transformation, called polarization, we get
\[ P2 = \epsilon^2\le \epsilon \le 2\epsilon-\epsilon^2 = P_1, \epsilon \in [0, 1] \] If we make U1 be the frozen bit, and U2 be the info bit, the erasure probability of U2 can be decreased.

Then we consider a new channel that has 4 bits and the erasure probabilities are \[ \begin{align*} & P_{1}' = 1 - (1 - P_1)^2 = 1 - (1-\epsilon)^4 \\ & P_{2}' = 1 - (1 - P_2)^2 = 1 - (1 - \epsilon^2)^2 \\ & P_{3}' = {P_1}^2 = (\epsilon^2 + 2\epsilon)^2 \\ & P_{4}' = {P_2}^2 = \epsilon^4 \\ \end{align*} \] As shown in the equation, the fourth bit gets a lower erasure probability.

It can be proved that polar codes are capable of achieving channel capacity as code length approaches positive infinity.

Compare

Based on the analysis, Compared with the Turbo code system, the LDPC system has many advantages.

1. low system complexity, low time delay and easier hardware implementation
2. better frame error ratio performance
3. error-floor is greatly reduced to meet the demand of extremely low error rate for communication system
4. the decoder has smaller power, adopts parallel decoding, and has a higher data throughput.

But LDPC codes are not a complete alternative to turbo code, It is concluded that the turbo code has better performance in moderate code rate (Rate 1/2) while the LDPC is recommended for higher code rates (3/4,7/8) because it has better performance beside less complexity compared with turbo code. For turbo code, all code rates require the same decoding complexity since all code rates are obtained from the mother code via puncturing. In contrast, the LDPC decoding complexity decreases as the code rate increases.

Compared with the LDPC, Turbo code system, the polar codes has several advantages.

1. A higher SNR will definitely result in a lower error rate in a polar code system.
2. Its coding and decoding complexity is low. When the coding length is N, the complexity is only O(NlogN).

Compared with polar codes, the LDPC system also has some advantages.

1. LDPC has developed for many years and the infrastructure is relatively well developed while Polar code is still a new technology.
2. systems using multivariate LDPC have better band utilization, and they also perform better in middle and shorter code length than Polar code.

Application

International Standard

IEEE 802.16, a wireless metropolitan network standard, uses block turbo coding and convolutional turbo coding.

Three application scenarios have been identified by the 5G standard: eMBB (improved mobile broadband), mMTC (large connected Internet of things), and URLLC (ultra-reliable ultra-low latency communication). eMBB stands for high-traffic mobile broadband, such as 3D ultra-high-definition video, mMTC stands for large-scale Internet of things business, and URLLC stands for services needing low-delay and high-reliability connections, such as manless driving and industrial automation. The LDPC code was established as a long block coding method for mobile broadband eMBB scenario business data channel coding at the 3GPPTSGRANWG1 conference in October 2016. The control channel coding method for the 5G short block of the eMBB scenario was determined to employ Polar code in November 2016 at the 3GPPRAN1 meeting.

The WiFi standard 802.11ac has embraced LDPC as a channel coding standard. In 2003, an irregular repeat accumulates (IRA) type LDPC code defeated six turbo codes to become the error-correcting code in the new DVB-S2 digital television satellite transmission standard. The ITU-T G.hn standard chose LDPC over convolutional turbo codes as the forward error correction (FEC) system in 2008. G.hn chose LDPC codes over turbo codes due to their lower decoding complexity (particularly at data rates near 1.0 Gbit/s) and the fact that the proposed turbo codes had a large error floor over the specified range of operation. 10GBASE-T Ethernet, which transfers data at 10 gigabits per second over twisted-pair lines, also uses LDPC codes. As of 2009, LDPC codes are also part of the Wi-Fi 802.11 standard as an optional part of 802.11n and 802.11ac, in the High Throughput (HT) PHY specification.

Application Scenarios

Turbo codes are used in many ways.

1. extensively in 3G and 4G mobile telephony standards; e.g., in HSPA, EV-DO, and LTE.
2. MediaFLO, terrestrial mobile television system from Qualcomm.
3. The interaction channel of satellite communication systems, such as DVB-RCS and DVB-RCS2.
4. Recent NASA missions such as Mars Reconnaissance Orbiter use turbo codes as an alternative to Reed–Solomon error correction -Viterbi decoder codes.

LDPC codes also have lots of applications.

1. In 5G NR (New Radio) LDPC codes are used for the data channel.
2. satellite transmission
3. Ethernet and WiFi
4. Even at low bit error rates, some OFDM systems incorporate an extra outside error correction that addresses the infrequent errors that slip past the LDPC rectification inner code. For instance: A Reed-Solomon outer code is used in the Reed-Solomon code with LDPC Coded Modulation (RS-LCM). The BCH code outer code is used in the DVB-S2, DVB-T2, and DVB-C2 standards to mop up leftover errors following LDPC decoding.

Polar codes have wide applications in Information theory such as Quasi Cyclic LDPC code, Irregular Repeat-Accumulate (IRA) code, Spatially Coupled LDPC (SP-LDPC), and NBLDPC Codes described.

Contributions of China

China's Huawei company has been developing Polar code for many years and has made great achievements in the development of coder and decoder of Polar code. Huawei has solved the basic problems of coding construction and decoding after two years of research. According to the latest public 14 years of technical information, IS selection problems, code length problems, decoding algorithms, HARQ, etc. also did not get a good solution.

Huawei has promoted the Polar Code (Polarization Code) scheme as the coding scheme for 5G control channel eMBB scenarios which can't be separated from China's growing comprehensive national power, as well as the communication and coordination of relevant domestic departments - in the most critical vote, Huawei's old domestic rival ZTE gave strong support, China Telecom, China Mobile, China Unicom, and Datang Telecom also chose to support Huawei. This marks a higher voice for Chinese communication vendors in the 5G era and reflects the growing strength of Chinese communication technology.

Future tendency

5G phones must support at least 4G and 3G networks from a device implementation standpoint. Turbo code is used in 3G and 4G, whereas LDPC and Polar code have been confirmed for 5G, implying at least three sets of coders and decoders on the phone. The baseband processor's coder and decoder are critical components. This design will raise the baseband processor's load and power consumption, reducing standby time and raising the cost of a 5G terminal. Operators' operating equipment, on the other hand, is incapable of smoothly transitioning from 4.5G to 5G, necessitating investment in new network equipment. which may also delay the formal commercial time of 5G.

Increasing the performance of future wireless systems requires the use of increasingly complicated channel codes, and this article outlines some of the high-level benefits. The application of Polar code will become more and more mature in the future, and there is a chance that other coding methods approaching or achieving the Shannon limit will be developed.

1. https://www.youtube.com/watch?v=zYOXFt0Ixwk ↩︎